
International Journal of Jaina Studies
(Online) Vol. 11, No. 2 (2015) 1-21
Abstract
This paper brings the formula d = S ÷ n²k into light and discusses its various aspects including its context in Jaina philosophy. It was set forth and utilized by Nemicandra (c. 981) in the Gommaṭasāra (Karmakāṇḍa) in order to demonstrate the lower-thought-activity (adhaḥ pravṛtta karaṇa). The lower-thought-activity is conceived as a special process of thought-concentration which causes destruction (kṣapaṇa) or suppression (upaśamana) of the sub-classes of conduct-deluding karma. The paper also offers a rationale for this specific formula. The relevance of the formula lies in the fact that it can be used for generating various arithmetic progressions by finding the common differences, d, in accordance with various values of an arbitrary number, k, while their sums, S, and the numbers of their terms, n, remain fixed. This way he used it. It can also be used for generating various arithmetic progressions by finding in accordance with various values of k while n and d remain fixed and by finding n in accordance with various appropriate values of k while S and d remain fixed.
A Specific Rule in India for Common Difference as Found in the Gommaṭasāra of Nemicandra (c. 981)
1. Introduction
Ācārya Nemicandra "Siddhānta Cakravartī" was a Digambara Jaina monk. He authored a number of works which became authoritative reference books for the Digambara Jaina tradition. The world famous colossal image of Bāhubalī was erected by his disciple Cāmuṇḍarāya, who has been a celebrated commander-in-chief and wise minister of the Gaṇga dynasty during the period from 953 to 985, at Śravaṇabeḷagoḷa in India. The first consecration ceremony of the statue was held on 13th March of 981. Nemicandra is said to have been in attendance there.[1]
The Jaina canons mainly deal with two systems. One is the system of karma where karma is the matter, exceptionally subtle, which actually does flow into the jīva (soul) and the other is the system of cosmology. Two treatises of Nemicandra's authorship are the Gommaṭasāra ('an essence extracted from the previous sources on the karma system and composed for Gommaṭa i. e. Cāmuṇḍarāya[2]') and the Trilokasāra ('essence of the three regions of the universe'). Both of them are post-canonical texts and written in Prakrit. The Gommaṭasāra deals with the karma system while the Trilokasāra deals with the Jaina system of cosmology and cosmography. The Gommaṭasāra has two sections: the Jīvakāṇḍa ('section regarding soul') and the Karmakāṇḍa ('section regarding karma'). The Trilokasāra is in only one section.
A lot of mathematical rules have been embedded by Nemicandra into these two treatises to apply them to solve the problems related with the respective systems. One of them is a specific rule offered by him in the Gommaṭasāra (Karmakāṇḍa) to find the common difference of an arithmetic progression. This rule is, as far as the present author knows, not found in any other treatise authored by either Nemicandra's predecessor or his successor. It remained unnoticed by historians of mathematics and will be brought into light and discussed in this article for the first time. We shall also offer a rationale for it in the section four of this paper. Before we take up it, we need to introduce the terms related with arithmetic progression [A. P.] and offer a brief survey of the history of its development in ancient and medieval Indian mathematics prior to him.
If S be the sum of an A. P. of n terms, then
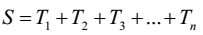 | [1] |
Where
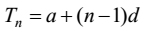 | [2] |
where a and d are its first term and common difference respectively. It means T1 = a.
We can write [1] as follows
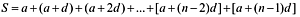 | [3] | |
| or | 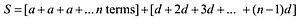 | |
| or | 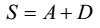 | [4] |
Where
| A=na | [5] |
is called the sum of the first terms of the A. P. and
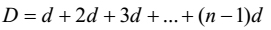 | [6] |
is called the sum of the common differences of the A. P.
Writing the A. P. [3] in reverse order, we have
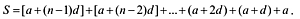 | [7] |
Adding [3] and [7], we get
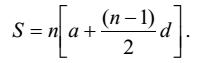 | [8] |
Indian interest in A. P. started quite early in the Vedic age. Quite a few instances are found in the Taittirīya Saṃhitā, the Vājasaneyī Saṃhitā, and other texts.[3] According to A. N. Singh, Indians must have obtained the formula for finding S at a very early date, but when exactly cannot be said for certain. It is, however, certain that in the period extending from 500 BCE to 400 BCE it was known, for in the Bṛhaddevatā, which is a summary of the deities and myths found in the Ṛgveda and is attributed to Śaunaka, we find S = 500499 for the A. P.: 2, 3, 4, , 1000.[4] The rule for finding S in terms of a , d , n is given in the Bakṣālī (usually spelt Bakhshali) Manuscript (c. 400 or 7th century).[5] The rules on A. P. referred to by some prominent authors of early medieval India can be observed from Table I.
Table I
| S. No. | The rule referred to | |||
| by the author | in the treatise | for | in terms of | |
| 1. | Āryabhaṭa I (born 476) | Āryabhaṭīya[6] | S | a , d , n |
| S | a , Tn , n where Tn is the n th term or the last term (antyadhana) of an A. P. | |||
| Āryabhaṭīya[7] | S | a , d , S | ||
| 2. | Yativṛṣabha (some period between 176 and 609) | Tiloyapaṇṇatti[8] | S | a , d , n |
| Tiloyapaṇṇatti[9] | d | a , n , S | ||
| Tiloyapaṇṇatti[10] | n | a , d , S | ||
| Tiloyapaṇṇatti[11] | S | a , d , n , i where i is an optional number (iṭṭha, Skt. iṣṭa). | ||
| Tiloyapaṇṇatti[12] | S | a , d , n | ||
| 3. | Brahmagupta (c. 628) | Brāhma-sphuṭa-siddhānta[13] | Tn | a , d , n |
| M | a , Tn | |||
| S | n , M where M (= (Tn + a) / 2) is its middle term (madhyadhana). | |||
| Brāhma-sphuṭa-siddhānta[14] | n | a , d , S | ||
| 4. | Śrīdhara (c. 799) | Pāṭīgaṇita[15] | S | a , d , n |
| S | a , Tn , n | |||
| Pāṭīgaṇita[16] | a | d , n , S | ||
| d | a , n , S | |||
| Pāṭīgaṇita[17] | n | a , d , S | ||
| Triśatikā[18] | Tn | a , d , n | ||
| M | a , Tn | |||
| S | n , M | |||
| Triśatikā[19] | a | d , n , S | ||
| d | a , n , S | |||
| Triśatikā[20] | n | a , d , S | ||
| 5. | Mahāvīra (c. 850) | Gaṇita-sāra-saṅgraha[21] | S | a , d , n |
| Gaṇita-sāra-saṅgraha[22] | A | a , n | ||
| D | d , n | |||
| S | A , D | |||
| Gaṇita-sāra-saṅgraha[23] | Tn | a , d , n | ||
| M | a , Tn | |||
| S | n , M | |||
| Gaṇita-sāra-saṅgraha[24] | n | a , d , S | ||
| Gaṇita-sāra-saṅgraha[25] | d | S , A , n | ||
| a | S , D , n | |||
| Gaṇita-sāra-saṅgraha[26] | a | d , n , S | ||
| d | a , n , S | |||
| Gaṇita-sāra-saṅgraha[27] | d | a , n , S | ||
| Gaṇita-sāra-saṅgraha[28] | a | d , n , S | ||
| 6. | Āryabhaṭa II (c. 950 or sixteenth century)[29] | Mahāsiddhānta[30] | S | a , d , n |
| Mahāsiddhānta[31] | a | d , n , S | ||
| Mahāsiddhānta[32] | d | a , n , S | ||
| Mahāsiddhānta[33] | n | a , d , S | ||
| 7. | Nemicandra (c. 981) | Trilokasāra[34] | n | a , d ,Tn |
| Trilokasāra[35] | a | d , n ,Tn | ||
| Tn | a , d , n | |||
| S | a ,Tn , n | |||
| Trilokasāra[36] | S | a , d , n | ||
What is served in Table I from the Trilokasāra shows that Nemicandra (c. 981) was familiar with the rules on A. P.
[2] can be inverted as follows:
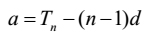 | [9] |
Let us see how he sets forth both [2] and [9] in the Trilokasāra. They are stated as follows:
vegapadaṃ cayaguṇidaṃ bhūmimhi muhammi riṇadhanaṃ ca kae |[37]
"Multiply the number of terms (pada, n ) of an A. P. as subtracted by one by the common difference (caya, d ). The product when subtracted from the last term (bhūmi, a ) yields the first term (muha, Skt. mukha, a ) and when added with the first term gives the last term of the A. P.."
Each of [2] and [9] can be inverted as follows:
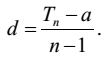 | [10] |
Let us see how he sets forth [8] in the Trilokasāra. It is stated as follows:
padamegeṇavihīṇaṃ dubhājidaṃ uttareṇa saṃguṇidaṃ |
pabhavajudaṃ padaguṇidaṃ padagaṇidaṃ taṃ vijāṇāhi || [38]
"The number of terms (pada, n ) of an A. P. is subtracted by one and then divided by two and multiplied by its common difference (uttara, d ). Add the result to the first term (pabhava, Skt. prabhava, a ) and then multiply the sum by the number of terms (pada, n ); know the product to be 'the sum of the n terms' (padagaṇida, Skt. padagaṇita, S ) of the A. P.."
The context in which the above two verses were furnished by him in the first chapter, lokasāmānyādhikāra ('general chapter on the universe'), of the Trilokasāra was to discuss indraka (central hole) and śreṇibaddhabilas (holes arranged in arithmetic progression).[39] This cosmographic context has nothing do with the subject at hand and its background described in the Gommaṭasāra (Karmakāṇḍa). [8] can be inverted as follows:
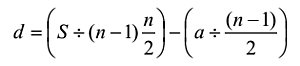 | [11] |
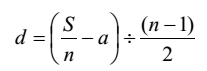 | [12] |
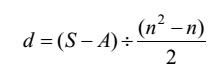 | [13] |
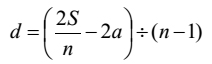 | [14] |
The rule for d in the shape of [11] was known to Yativṛṣabha.[40] It was known in the shape of [12] to Śrīdhara[41], Mahāvīra[42] and Āryabhaṭa II[43]. Mahāvīra knew it in the shape of [13] and [14] as well.[44]
This brief survey on A. P. enables us to assert that the rule, each of [10] and [11]/[12]/[13]/[14], for d must have been known to Nemicandra in one or the other shape. This was the very purpose of the survey.
2. The installation of the specific rule
In the Gommaṭasāra (Karmakāṇḍa) he sets forth a specific rule to find d as stated below:
ubhayadhaṇe saṃmilide padakadiguṇasaṃkharūvahadapacayaṃ |
savvadhaṇaṃ taṃ tamhā padakadisaṃkheṇa bhājide pacayaṃ ||[45]
"Both (ubhaya) 'the sum of the first terms', A , and 'the sum of the common differences', D, when added happen to be equal to the square of 'the number of terms' (pada, n ) as multiplied by an arbitrary number (saṃkha, Skt. saṅkhya, k (say)) and by the common difference (pacaya, Skt. pracaya, d ). Therefore, the sum (savvadhaṇa, Skt. sarvadhana, S ) being divided by the square of 'the number of terms' (pada, n ) and by an arbitrary number (saṃkha, Skt. saṅkhya, k ) gives rise to the common difference (pacaya, Skt. pracaya, d )."
That is to say:
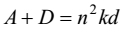 | [15] | |
| or | 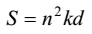 | |
| Therefore, | 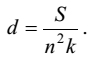 | [16] |
The first hemistich of the above verse contains [15] while [16] is embedded into its second hemistich. Since [16] contains k , it cannot be a general rule. It is required to be a specific rule. It enables us to find d when only S and n are known. Unlike [10] and [11]/[12]/[13]/[14] it is free from a . It is found nowhere in Table I. It has not been a part of the mainstream of the mathematics in India concerned with A. P.
3. The context of the rule
If each term of [1] is detached into an A. P. of m terms, then
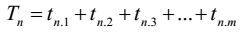 | [17] |
Where
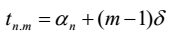 | [18] |
Where αn and ξ are its first term and common difference respectively. It means tn.1 =αn .
We can write [17] as follows
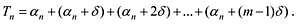 |
Then
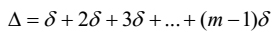 | [19] |
is called the sum of the common differences of the A. P. [17].
The context in which Nemicandra set forth [16] runs into sixteen verses, namely from 897 to 912 including the one stated above in the section two, of the chapter eight of the Gommaṭasāra (Karmakāṇḍa) (GSK). It is as follows: [46]
Thought-activity (karaṇa), in which a soul's pure thoughts increase infinite fold at every instant (samaya), is a special process of thought-concentration.[47] It is the instrumental cause for destruction (kṣapaṇa) or suppression (upaśamana) of twenty-one sub-classes of conduct-deluding (cāritra-moha) karma.[48] Among those twenty-one sub-classes are four partial-vow-preventing passions (apratyākhyānāvaranīya kaṣāya), four total-vow-preventing passions (pratyākhyānāvaranīya kaṣāya), four perfect-conduct-preventing passions (saṃjvalana kaṣāya) and nine quasi-passions (nokaṣāya, slight or minor passions). Each of the first three contains anger (krodha), pride (māna), deceit (māyā) and greed (lobha). And the nine quasi-passions are laughter (hāsya), indulgence (rati), ennui (arati), sorrow (śoka), fear (bhaya), disgust (jugupsā), feminine inclination (strī-veda), masculine inclination (puṃ- veda) and neither feminine nor masculine sexual inclination (napuṃsaka-veda).[49] Thoughtactivity is divided into three kinds. They are (1) the lower-thought-activity (adhaḥ pravṛtta karaṇa), (2) the new-thought-activity (apūrva karaṇa) and (3) the advanced-thought-activity (anivṛtti karaṇa).
(1) The lower-thought-activity is named so because using it the quality (bhāva) of a posterior soul may grow to be as pure as that of a prior soul. In other words, due to more extensive practice, a soul who has commenced purifying thoughts later may come up to the level of the soul who commenced the same earlier. In mathematical terms, on the path leading to purifying thoughts the rate of progress of a posterior soul may be higher than that of a prior soul. The lower-thought-activity is used by a soul in the perfect vow-stage (apramatta virati) which is the seventh of the fourteen guṇasthānas (qualitative stages of spiritual development), in which the embodied soul has all vows and keeps them perfectly. The lower thought-activity is performed not longer than one antara-muhūrta, that is, 48 minutes minus one samaya where samaya (instant) is an indivisible part of time. The increase of pure thoughts is theoretically calculated in terms of a uniform progression (sadṛśavṛddhi) (i. e., in A. P.).[50]
(2) Having passed the antara-muhūrta stage in the lower-thought-activity the soul is engrossed in the new-thought-activity, associated with the eighth guṇasthāna, where thoughts that had not arisen before arise. The duration of the new-thought-activity also is one antaramuhūrta. In the stage of new-thought-activity, if the souls commence purifying thoughts at the same instant, their progress onwards may be equal or unequal; but none of them can ever be overtaken by any soul who commences afterwards.[51]
(3) In the advanced-thought-activity, associated with the ninth guṇasthāna, the souls that commenced purifying thoughts at the same instant shall continue to go forward uniformly without any difference in the degree of purity. Here all the twenty-one sub-classes of conduct-deluding karma are destroyed or suppressed by the soul.[52]
In order to demonstrate the lower-thought-activity Nemicandra assumed[53]
 | [20] |
Here n is said to be the number of vertical terms (ūrdhvādhvāna), d the vertical common difference (ūrdhvaviśeṣa), m the number of horizontal terms (tiryagadhvāna), and ξ the horizontal common difference (tiryagviśeṣa).[54] See, in view of these data, Table II.
Firstly, he states that, according to his predecessors, in the lower-thought-activity D is numerable part of A .[55] That is to say: if
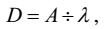 | [21] |
λ, in the light of the above data, comes to be 27 5. This result cannot be arrived at without knowing the rules for finding D and a . He incorporates them into the latter verses.
Secondly, he composes the rules for [15] and [16] into the verse which we have already noticed above in the section two.
Thirdly, for finding a he enunciates the formula,
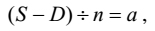 | [22] |
in the first hemistich of the following verse.
cayadhaṇahīṇaṃ davvaṃ padabhajide hodi ādiparimāṇaṃ |
ādimmi caye uḍḍhe paḍisamayadhaṇaṃ tu bhāvāṇaṃ || [56]
"The value (parimāṇa) of the first term (ādi, a ) is arrived at when 'the sum of the common differences' (cayadhaṇa, Skt. cayadhana, D ) is subtracted from the sum (davva, Skt. dravya, total number of thoughts that are to attain purity, S ) and then divided by 'the number of terms' (pada, n ). The number of thoughts (bhāva) that attained purity at each instant (samaya) is obtained by adding the common difference (caya, d ) in succession to this first term (ādi, a )."
In the second hemistich of the above verse he instructs how to prepare the required A. P. That A. P. can be seen in the first column of Table II. To find a using [22] it is essential that D must be known at the outset.
Fourthly, in order to educate how to calculate D he, equating the corresponding terms given in the right hand side of [6] with the formula [8], sets forth a rule as follows:
pacayadhaṇassāṇayaṇe pacaya pabhavaṃ tu pacayameva have |
rū^ūṇapadaṃ tu padaṃ savvatthavi hodi ṇiyameṇa||[57]
"In order to calculate 'the sum of the common differences' (pacayadhaṇa, Skt. pracayadhana, D ) of an A. P., the common difference (pacaya, Skt. pracaya, d ), the first term (pabhava, Skt. prabhava, a ) of the common differences, which is the same as the common difference (pacaya, Skt. pracaya, d ) is, and 'the number of terms less one' (rū^ūṇapada, Skt. rūponapada, (n-1)) to be assigned to 'the number of terms' (pada, n ) are always taken according to the rule (ṇiyama, Skt. niyama)."
That is to say: in order to calculate D ,
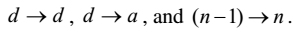 |
Accordingly,
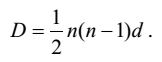 | [23] |
It may easily be understood that [22] is arrived at when [23] is subtracted from [8] and then divided by n . Using [16] d , in the light of S = 3072, n = 16, k = 3, comes to be 4. Then, using [23], D = 480. Subsequently, using [22], a = 162. By adding 4 to 162 in succession we get other terms of thoughts that attained purity. See the column one in Table II. In the later part of the context he talks about the sub-terms of thoughts.
Fifthly, he states that
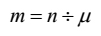 | [24] |
where μ is an arbitrary number. Here the terms used by him for m and n are aṇukaṭṭipada (Skt. anukṛṣṭipada, 'number of the terms (i. e. thoughts) that are ploughed along' if literally translated) and savvaddhāṇa (Skt. sarvādhvāna) respectively.[58] Since it is noticeable from [20] that m = 4 and n = 16, it can be easily inferred that he assumed μ= 4. This is why each term of the vertical A. P. is detached into four sub-terms. See Table II.
Sixthly, he states
 | [25] |
in the first hemistich of the following verse.
aṇukaṭṭipadeṇa hade pacaye pacayo du hoi tericche |
pacayadhaṇūṇaṃ davvaṃ sagapadabhajidaṃ have ādī ||[59]
"The vertical common difference (pacaya, Skt. pracaya, d ) when divided by the number of horizontal terms (aṇukaṭṭipada, Skt. anukṛṣṭipada, 'number of the terms (i. e. thoughts) that are ploughed along' if literally translated, m ) gives rise to the horizontal (tericche, Skt. tirśchi) common difference (pacaya, Skt. pracaya, ξ). 'The sum of the horizontal common differences' (pacayadhaṇa, Skt. pracayadhana, Δ) subtracted from the horizontal sum (davva, Skt. dravya, n T ) gives rise to the first horizontal term (ādi, n α) when divided by 'the own number of terms' (sagapada, Skt. svakapada, m )."
The second hemistich of the above verse contains
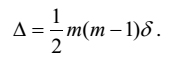 | [27] |
Let us see how to calculate α1. Using [25] ξ, in the light of d = 4, m = 4, comes to be 1. Then, using [27], Δ = 6. Subsequently, using [26], α1 = 39 as T1 = 162.
Seventhly and finally, he states that ξ is successively added to each term commencing from αn . Like this, a vertical and horizontal assortment (uḍḍhtiriyarayaṇā, Skt. ūrdhvatiryagracanā) should be known in the lower-thought-activity.[60] See Table II.
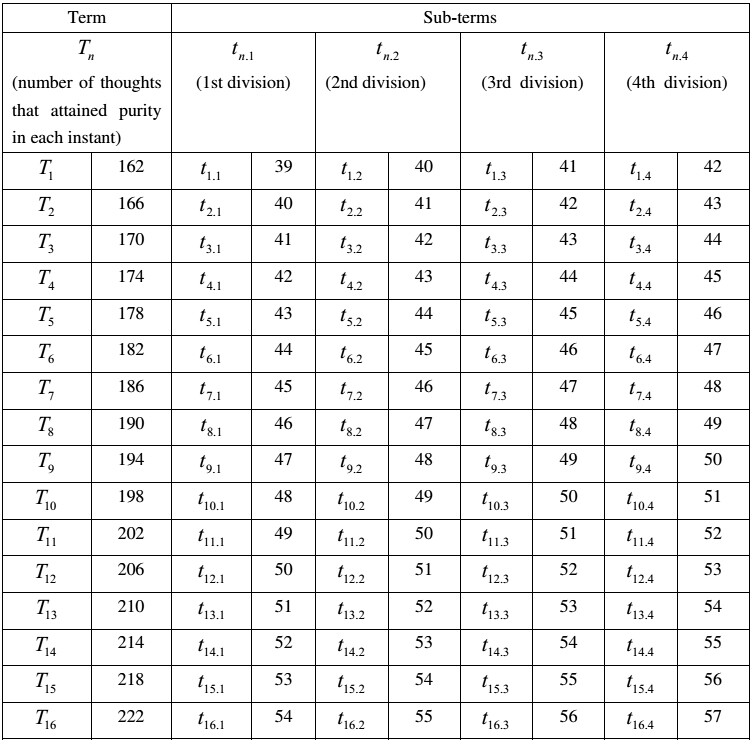 Table II
Table II
The following is an explanation offered by Sital Prasad regarding the horizontal terms shown in Table II:
"Let us assume that 4 persons have entered upon a stage of lower thoughtactivity one having 39, the other 40, the 3rd 41 and the 4th 42 steps in thought purity. Each is advancing every moment by one step. In the next instant the four will respectively have progressed to 40, 41, 42 and 43 steps. Then suppose that another set of four persons have entered upon such thought purity. They will have in the first instant, steps of 39, 40, 41 and 42. Here the person who has 40 in the first instant will be equal to that person who has 40 in the 2nd instant, and one who has 41 in the first instant will be equal to the person who has 41 in the 2nd instant. The one in the first group who has 39 in the first instant will have 42 in the 4th instant while the 4th person of the 2nd group has 42 in the first instant. Thus a person entering upon thought-purity later may be equal to one who has commenced earlier. Where such progress of increase of purity is possible, it is called the lower thought-activity."[61]
Because of having common characteristics the thoughts of the last three divisions in the first instant respectively match those of the first three divisions in the second instant. For the same reason the thoughts of the last three divisions in the second instant respectively match those of the first three divisions in the third instant and the same follows in the consecutive instants. Only the thoughts of the first division in the first instant and those of the last division in the last or sixteenth instant remain matchless. It means that the thoughts that are to appear to attain purity in the posterior instants are partly covered in the prior instants. This seems to be the plausible interpretation of aṇukaṭṭipada (Skt. anukṛṣṭipada, 'number of the terms (i. e. thoughts) that are ploughed along' if literally translated) in the lower-thoughtactivity. On the other hand, in the new-thought-activity m = 0 for at each instant innumerable number of new thoughts attain purity.[62] In the advanced-thought-activity one thought per instant attains purity.[63]
As far as the lower-thought-activity is concerned, it was known prior to Nemicandra in Jaina philosophy but the way in which he demonstrated it using mathematics, especially the rule [16], is not found in any treatise anterior to the Gommaṭasāra.[64]
4. Rationale for the rule
We have noticed above that there are three formulae that contain arbitrary numbers. One is [16] that contains k . The others are [`21] and [24] that contain λ and μ respectively. Both of them simply correspond to the ratio. k too may be regarded to be a ratio between S and n2d. But it is not usually expected that when one wants a ratio, he will hit upon such a consequent that contains the product of two terms, namely n and d, and one of them is with its square, namely n2, while its antecedent contains a single term, namely S. For this reason k seems to have been involved passing through some process on d, S and n. [25] cannot be compared with [16] for the former is a result of the ratio simply taken.
Now the question is how Nemicandra processed to hit on [16]. [15], especially its left hand side, does seem to be a clue in this matter. He serves it as a prior step to [16]. Using this clue we can suggest a rationale for [16]. Our rationale is as follows:
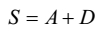 | ||
| or | 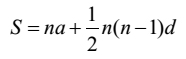 | |
| or | 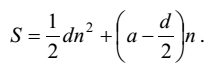 | [28] |
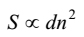 | ||
| or | 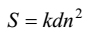 | [29] |
where 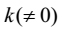 is an arbitrary number, which, when inverted, gives [16].
is an arbitrary number, which, when inverted, gives [16].
Although it is true that Indians had a sound knowledge of quadratic equations and the methods of their solutions by his time[65], we do not have, in fact we could not find, any evidence, especially that S dn 2 was known, to substantiate that the method employed in our rationale may have been literally used by Nemicandra. However, our rationale does suggest that [16] is a rule, certainly of specific nature, for finding d as it can be obtained by way of processing on d , S and n .
5. Relevance of the rule
To determine d one needs the value of k besides S and n , and when one does select the value of k then d is calculated using [16] and thereafter a is calculated using [23] for the intermediate purpose and [22] for the purpose. It means that k is not only directly related with the computation of d but also ultimately determines a . In this sense too [16] is specific.
For other values of k than 3 we shall have a variety of assortments. For the reason that the formulae [24] and [25] are not derived using any process, our mathematical interest does not lie in the formation of the horizontal terms (i. e. the sub-terms of thoughts). It does, because of [16], lie in the formation of the vertical terms. Table III contains various arithmetic progressions in accordance with various values of k while S(= 3072) and n(= 16) are fixed. In the context of the above sort, k would not take any negative number. On the other hand, we have assigned negative numbers to k in Table III so that we can view a larger use of [16]. For the same purpose [11]/[12]/[13]/[14], which needs a to determine d , may be used but in that case we shall have to choose the value for a . For the employment of [10] we shall have to choose not only a but also Tn . On the other hand, Nemicandra seems to have "fed two birds", d and a , "with one scone", k , that too in a methodical manner. Hence [16] can be applied to a system similar to the lower-thought-activity.
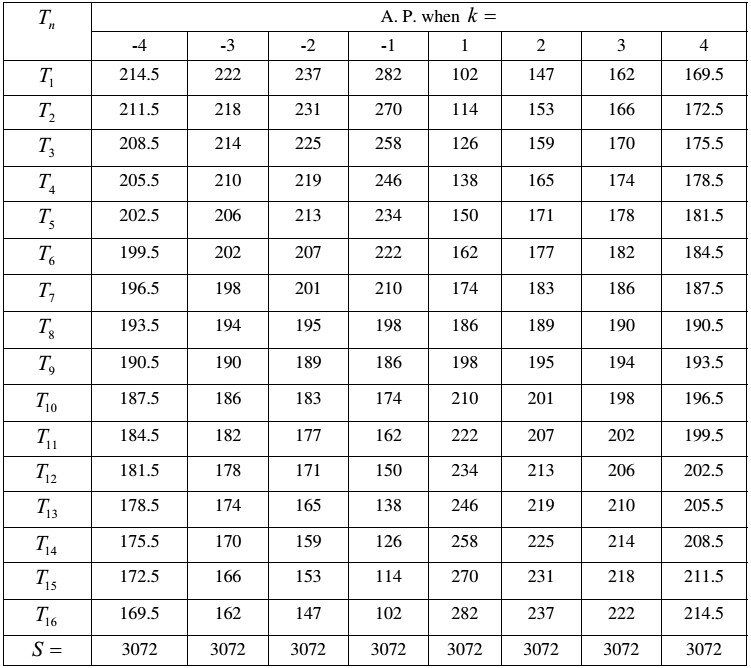 Table III
Table III
[29] seems to have been first obtained as both the entire verse referred to by Nemicandra for [16] and our rationale suggest. We can use [29] to generate various arithmetic progressions by finding S in accordance with various values of k while n and d remain fixed. See Table IV.
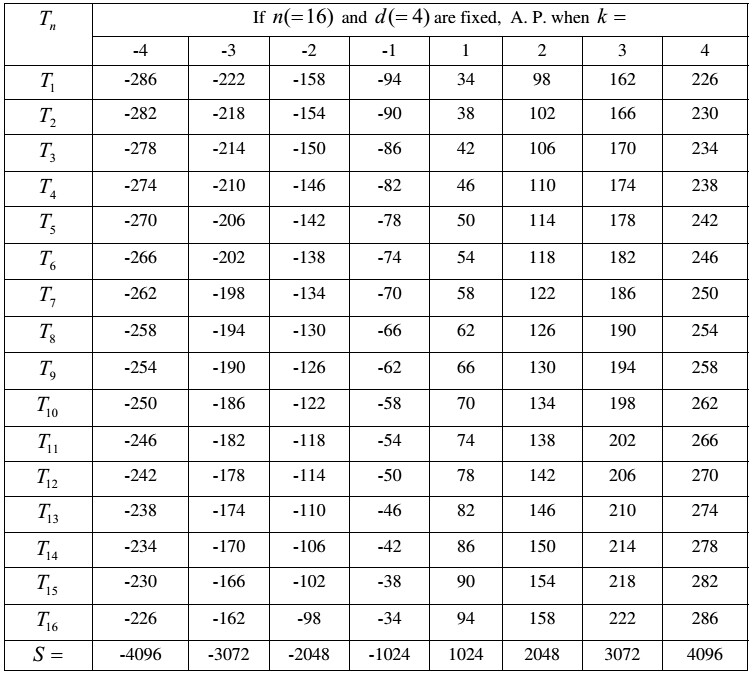 Table IV
Table IV
[29] can be inverted as follows:
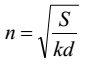 | [30] |
It can be used to generate various arithmetic progressions by finding n in accordance with various appropriate values of k while S and d remain fixed. See Table V.
6. Concluding remarks
There seems to have been two rules before Nemicandra for finding d . One rule [10] is in terms of a , n , n T . It could not be utilized by him for in the lower-thought-activity neither a , the number of thoughts that are to attain purity in the first instant, nor n T , that of thoughts that are to attain purity in the n th or last instant, is predetermined. The other rule was [11]/[12]/[13]/[14] or the like. [11]/[12]/[14] is in terms of a , n , S while [13] is in terms of A , n , S . These variants too could not be employed by him, for in the lower-thought-activity both n , the number of instants at each of which purity is to be attained by thoughts, and S ,
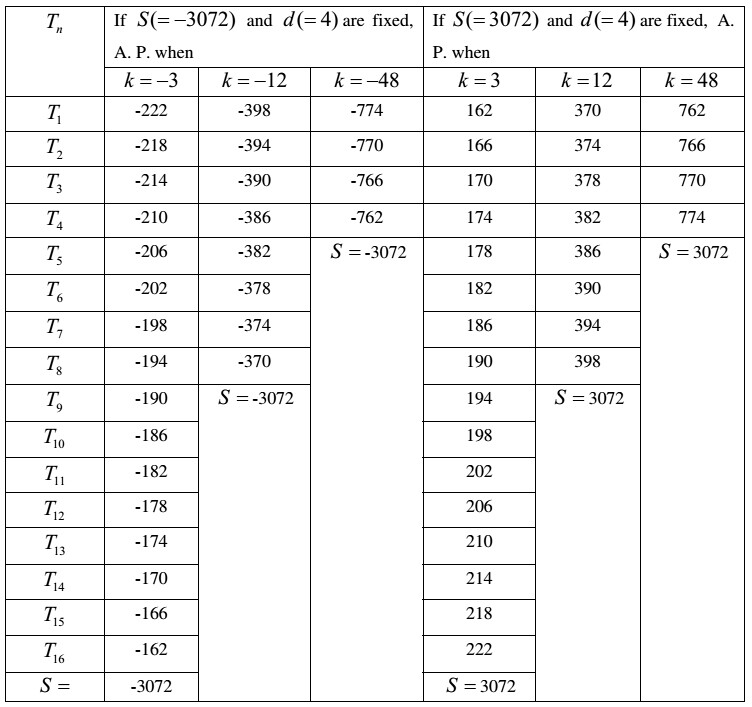 Table V
Table V
the total number of thoughts that are to attain purity, are fixed, but a is not predetermined. Since, in [16], d is inversely proportional to k , d will increase when k decrease. We are able to observe this if we go by Table III. It also shows that the values of a decrease when those of k decrease. It is k which maintains d and a in the above manner. A rule having this sort of feature was required for the demonstration of the lower-thought-activity, especially its important facet that the rate of progress of a posterior soul may be higher than that of a prior soul on the path leading to purifying thoughts. And for that particular purpose [16] was created in mathematics for the service of Jaina philosophy.
ACKNOWLEDGEMENTS
The author is grateful to the one anonymous learned scholar in the field and the learned referees and the learned editor of this journal for their helpful suggestions and valuable comments.
BIBLIOGRAPHY
Primary Sources
ĀB Āryabhaṭīya, by Āryabhaṭa I. With the Commentary of Bhāskara I and Someśvara. Edited by K. S. Shukla. New Delhi: Indian National Science Academy, 1976.
BSS Brāhmasphuṭasiddhānta, by Brahmagupta. Vol. II. Edited by R. S. Sharma & Team. New Delhi: Indian Institute of Astronomical and Sanskrit Research, 1966.
Dhavalā Dhavalā, by Vīrasena. A Commentary on the Ṣaḍkhaṇḍāgama of Puṣpadanta and Bhūtabalī. Section I, Part I, Book I. Edited and Translated in Hindi by H. L. Jain et al. Solapur: Jaina Saṃskṛti Saṃrakṣaka Saṅgha, 1940-50/2000.GSK1 Gommaṭasāra (Karmakāṇḍa), by Nemicandra. Along with Karṇāṭavṛtti Jivatattvapradīpīkā. Vol. II. Edited by A. N. Upadhye & K. C. Shastri. New Delhi: Bhāratīya Jñānapīṭha Publication, 1996.
GSK2 Gommaṭasāra (Karmakāṇḍa), by Nemicandra. In Gommatsara Karma-Kanda: Part II [vv. 398-972]. Edited With an Introduction, Translation, and Commentaries by Brahmachari Sital Prasad, Assisted by Pandit Ajit Prasad. Lucknow: The Central Jaina Publishing House, 1937 (The Sacred Books of the Jainas 10).
GSJ Gommaṭasāra (Jīvakāṇḍa), by Nemicandra. Edited and Translated into English by J. L. Jaini. Lucknow: The Central Jaina Publishing House, 1927.
GSS Gaṇitasārasaṅgraha, by Mahāvīra. With Notes and Translation into English by M. Rangacharya, 1912. Edited and Translated into Kannada by Padmavathamma. Hombuja: Siddhārtakirti Granthamālā, 2000.
MS Mahāsiddhānta, by Āryabhaṭa II. Edited by Sudhakara Dvivedi. Delhi: Chaukhamba Sanskrit Pratishthan, 1995.
PG Pāṭīgaṇita, by Śrīdhara. Edited by K. S. Shukla. Lucknow: Department of Mathematics and Astronomy, Lucknow University, 1959.
TP Tiloyapaṇṇatti, by Yativṛṣabha. Part I. Edited by C. P. Patni. Dehra-Tijara: Candraprabha Digambara Jaina Atiśayakṣetra, 1997.
TS Trilokasāra, by Nemicandra. With Mādhavacandra Traividya's Sanskrit Commentary and with Āryikā Viśuddhamatī's Hindī Commentary). Edited by R. C. Jain Mukhtara & C. P. Patni. Mahāvīrajī, 1975.
TŚ Triśatikā, by Śrīdhara. Edited by Sudhakara Dvivedi. Benares: Chandraprabha Press, 1899.
Secondary Sources
Bag, A. K. Mathematics in Ancient and Medieval India. Varanasi: Chaukhamba Orientalia, 1979.
Datta, B. B. "Mathematics of Nemicandra." The Jaina Antiquary 1, 2 (1935) 25-44.
Datta, B. B. & A. N. Singh. History of Hindu Mathematics. Part II. Lahore: Motilal Banarsidas, 1938.
Datta, B. B. & A. N. Singh. "Use of Series in India (Revised by K. S. Shukla)." Indian Journal of History of Sciences 28, 2 (1993) 103-129.
Hayashi, Takao. The Bakhshālī Manuscript. Ph. D. Dissertation, Brown University, 1985.
Jadhav, Dipak. "Gommaṭasāra kā Nāmakaraṇa." Arhat Vacana 11, 4 (1999) 19-24.
Jadhav, Dipak. "On the Sum of an A. P. with Optional Number in Ancient India." Arhat Vacana 17, 2-3 (2005) 53-57.
Jadhav, Dipak. "Why do I assign 981 A. D. to Nemicandra?" Arhat Vacana 18, 1 (2006) 75- 81.
Jadhav, Dipak & N. Shivakumar. "On the Peculiar Formula for finding the Sum of an A. P. in India." Arhat Vacana 17, 4 (2005) 47-51.
Jaini, Jagmander Lal. Jaina Gem Dictionary. Arrah: The Central Jain Publishing House, 1918.
Macdonell, Arthur Anthony. The Bṛhaddevatā (Part I: Introduction and Text and Appendices and Part II: Translation and Notes). Massachusetts: Harvard University, 1904.
Mercier, Raymond. "The Date of the Mahāsiddhānta." Gaṇita Bhāratī 15, 1-4 (1993) 1-13.
Pingree, David. "On the Date of the Mahāsiddhānta of the Second Āryabhaṭa." Gaṇita Bhāratī 14, 1-4 (1992) 55-56.
Sewell, Robert. The Siddhantas and the Indian Calendar. Calcutta: Central Publication Branch, Government of India, 1924.
Singh, A. N. "On the use of Series in Hindu Mathematics." Osiris 1 (1936) 606-628.
© The Editor. International Journal of Jaina Studies (Online) 2015
Singh 1936: 608. Also see Datta &Singh 1993: 104. See also Macdonell 1904: Part I, śloka 3.130, 35 and Part II, 117.
GSK2 vv. 897-899 and Sital Prasad's comments, pp. 285-7. For verses 47, 48 and 49 of the GSJ being identical with verses 897, 898 and 899 of the GSK see GSJ vv. 47-99 and Jaini's comments, pp. 37-44. For the meaning of bhāva see Jaini 1918: 33. For a brief account of spiritual stages see GSJ vv. 1-69, pp. 1-51. For antaramuhūrta see Jaini 1918: 17. The expression 'pure thoughts' refers to 'the number of pure thoughts.' The explanation found in the commentary on the GSK for the latter is viśuddhi-kaṣāya-pariṇāma, 'the number of passions that are purified out or removed out' if translated literally.' See GSK1 below v. 899, p. 1250.
GSJ vv. 50-53, pp. 39f. and 44, and GSK2, p. 286. Verse 50 of GSJ is identical with verse 908 of GSK.
GSJ vv. 54-57, pp. 40f. and 44, and GSK2, p. 286. Verse 56 of GSJ is identical with verse 911 of GSK.
Nemicandra, Gommaṭasāra (Karmakāṇḍa) (Ed. Upadhye and Shastri), v. 900 and its commentary, pp. 1250f.
 Dipak Jadhav
Dipak Jadhav
