Jaina Mathematics and its Cultural Underpinnings

I feel honoured to accept the invitation for a 20 minute lecture on Jaina Mathematics and its cultural underpinnings. The title, honestly speaking, calls for a whole book, for thorough discussion. All, I therefore can do here today is to give you a sharp outline.

The Mathematical heritage of India, historically speaking is nearly 3000 yrs. Old. The Jain philosophy, which is non-absolutist in nature, is certainly not out of this heritage, the heritage which is a vital part of its cultural underpinnings.

To those in the audience, who might not have necessary information about this age-old philosophy. I address myself by saying that the Jaina religious literature has broad classifications which, taken as a whole, are known as Anuyogas. Each Anuyoga individually, explains the salient principles of Jainism. According to Śwetāmbara sect these are:

1. Dharmakathānuyoga

2. Caraṇakarṇānuyoga

3. Gaṇitānuyoga

4. Dravyānuyoga^[1].

Meanwhile, I want to be excused, that in the absence of connotative English terms, I have had to use, the original Jain terms with their approximate English equivalents.

The knowledge of Saṅkhyā, i.e. the science of numbers, in relation to arithmetic and astronomy, is considered as one of the principal accomplishments of the Jain Priests. It is to be noted that the Jaina's attribute to the founders including of course Lord Mahāvīra of their religion a sound knowledge of those sciences. According to them one should be taught firstly writing, followed by a knowledge in arithmetic, as two of the important sciences from among seventy two arts (śilpas)^[2]

There are two notable astronomical treatises called the Suryaprajñapti and the Candraprajñapti. There were certainly some more treatises by the early Jaina scholars, unfortunately, some of them are lost. But Śrīdharkṛta Pāṭī Gaṇita, Gaṇita Sara Sangraha by Mahāvīra Ācārya (AD 850) Gaṇita Tilak (AD 1039), Līlāvatī (AD 1150), Ganita Kaumudi (AD 1356) and some more are however, available at present.^[3]

We can get much useful information about the Jaina's knowledge of Mathematics from the various Ardha-Māgadhi religious and secular books. For instance, the commentator Śīlānka (AD 862) is found to have quoted three verses bearing on permutations and combinations which, however, cannot be traced to any available treatise on Mathematics. Thanks to Bibhuti Bhusan Dutta, who in his article, 'Jaina School of Mathematics' published in the year 1929 has noted this point.^[4]

Classification of numbers into odd and even occurs in the Jaina canonical works. Jainas do not consider unity a number 'eko gaṇanā saṅkhyā na upaiti'. Such was also the case with the early Greeks. According to Ācārya Mahāprajña no importance is attached to number one in Jaina philosophy 'saṅkhyati iti saṅkhyā '^[5] i.e. number that can be divided is a number.

Please note that Sūtra no. 574 of A Jain treatise named Anuyogadvāra, clearly states that a unity does not make numeration. Numeration starts with a number 2 and goes on and on.^[6] It may also be pointed out that Parama Śunya has not been given consideration in Jaina philosophy.^[7]

The classification of number is this: Sāṅkhyea i.e. numerable, Asaṅkhyeya innumerable and Ananta i.e. infinite.^[8] The numerables are known to be of three types, such as Jaghnya (lowest), Utkṛṣṭa (highest) and Ajaghanya-anutkṛṣṭa (neither high nor low) i.e. intermediate.^[9]

Likewise, innumerables are also of three kinds such as Parīta asaṅkhyeya (nearly innumerable) Yukta asañkhyeya (truly innumerable) Asaṅkhyeya asañkhyeya (innumerably innumerable). Again, nearly innumerable, truly innumerable and innumerably innumerable each one of them is classified in three types - lowest, highest and intermediate.^[10]

Infinites are also of 3 types. The first two types are Parīta ananta (nearly infinite) Yukta ananta (truly infinite) have three such gradations lowest, highest and intermediate. But Anantānanta (infinitely infinites) are of only two orders: lowest and intermediates."^[11]

It shows that in Jaina philosophy there is no place for highest infinitely infinite. The subject is quite abstruse for a time bound lecture. But I hope, that the fact why Jaina philosophy is non-absolute can be understood only if we care to study Jaina Mathematics.

According to Sthānāṅga Sūtra^[12], A Jaina canonical work of 300 B.C. or still earlier, the topics for discussion in Mathematics are ten in number: Sri B.B. Dutta, in his article already referred by me, has taken note of this point. These are:

• Parikarma i.e. fundamental operations
• Vyavahāra i.e. subjects of treatment According to Brahmadatta there are 8 types of Vyavahāra in Pāṭī-Ganita
• Rajju i.e. rope, meaning geometry
• Rāshi i.e. heap, meaning mensuration of solid bodies.
• Kalāsavarṇa i.e. fractions.
• Yāvat tāvat i.e. as many as, meaning simple equations.
• Varga i.e. square, meaning quadratic equations.
• Ghana i.e. cube, meaning cubic equations.
• Vargavarga i.e. biquadratic equations.
• Kalpa permutations and combinations.

In Anuyogadvāra Sūtra we find three units of measurement in terms of aṅgula (finger-breadth) Śucya aṅgula (needle-like finger), Pratara aṅgula (plain finger) and Ghana aṅgula (solid finger). It is stated further, that the Śucya aṅgula is linear and one dimensional; Śucya aṅgula multiplied by Śucya aṅgula gives Pratara aṅgula and Pratara aṅgula multiplied by Śucya aṅgula becomes Ghana aṅgula, also occur in other canonical works. Hence, those terms define respectively the units of linear, superficial and solid measures.^[13]

In Anuyogadvāra Sūtra we find the geometrical figures Tṛasra (triangle), Caturasra i.e. quadrilateral, Āyata i.e. rectangle, Vṛtta i.e. circle and Parimanḍala i.e. ellipse.^[14]

Now each of these is further classified into two kinds Pratara (plain) and Ghana (solid). Ghana Tṛasra denotes a triangular pyramid, Ghana Caturasra a cube, Ghana Āyata a rectangular parallelepiped, Ghana Vṛtta a sphere and Ghana Parimanḍala an elliptic cylinder. Reference to these figures also occur in other Jaina canonical works such as Jambudvīpa Prajñapti, Jīvābhigam Sūtra, Bhagavatī Sūtra etc.

However, an illustration would clarify the intricacies, involved in these divisions. From the Aruṇvara Ocean of middle world, Madhya Loka rises dense water vapour called Tamaskāya, which reaches upto the third layer of Brahma Loka i.e. fifth heaven. Here in Brahma Loka we can see eight black-fields (these are 8 Kṛṣṇa Rājīs. In this picture we can see 2 triangular, 2 hexagonal and 4 rectangular shapes. These Krsna Rājīs are made up of earth bodies. The water vapour of Tamaskāya,, which rises from the ocean, mixes with Krsna Rājīs. Here sometimes Devtās or enemies of Devtās try to hide themselves, once they get into it, it is very difficult for them to come out of it. You could say that these Krsna Rājīs, are equivalent to the Black hole of today.^[15]

This leads us to a consideration of Loka. Mathematics has been so used in Jain philosophy as to be instrumental to explain these eternal substances of the Loka, universe.

This is a picture of Loka

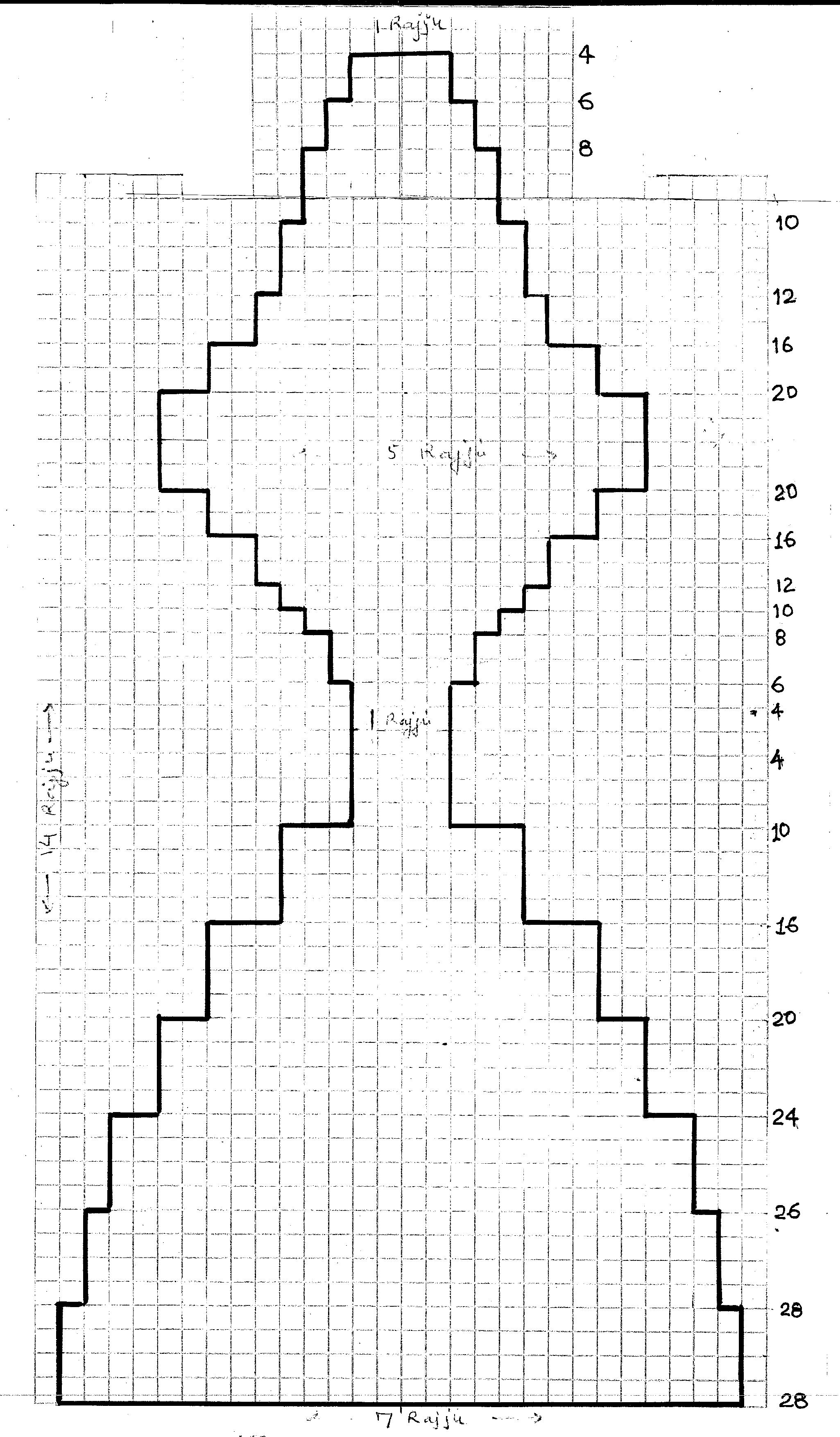
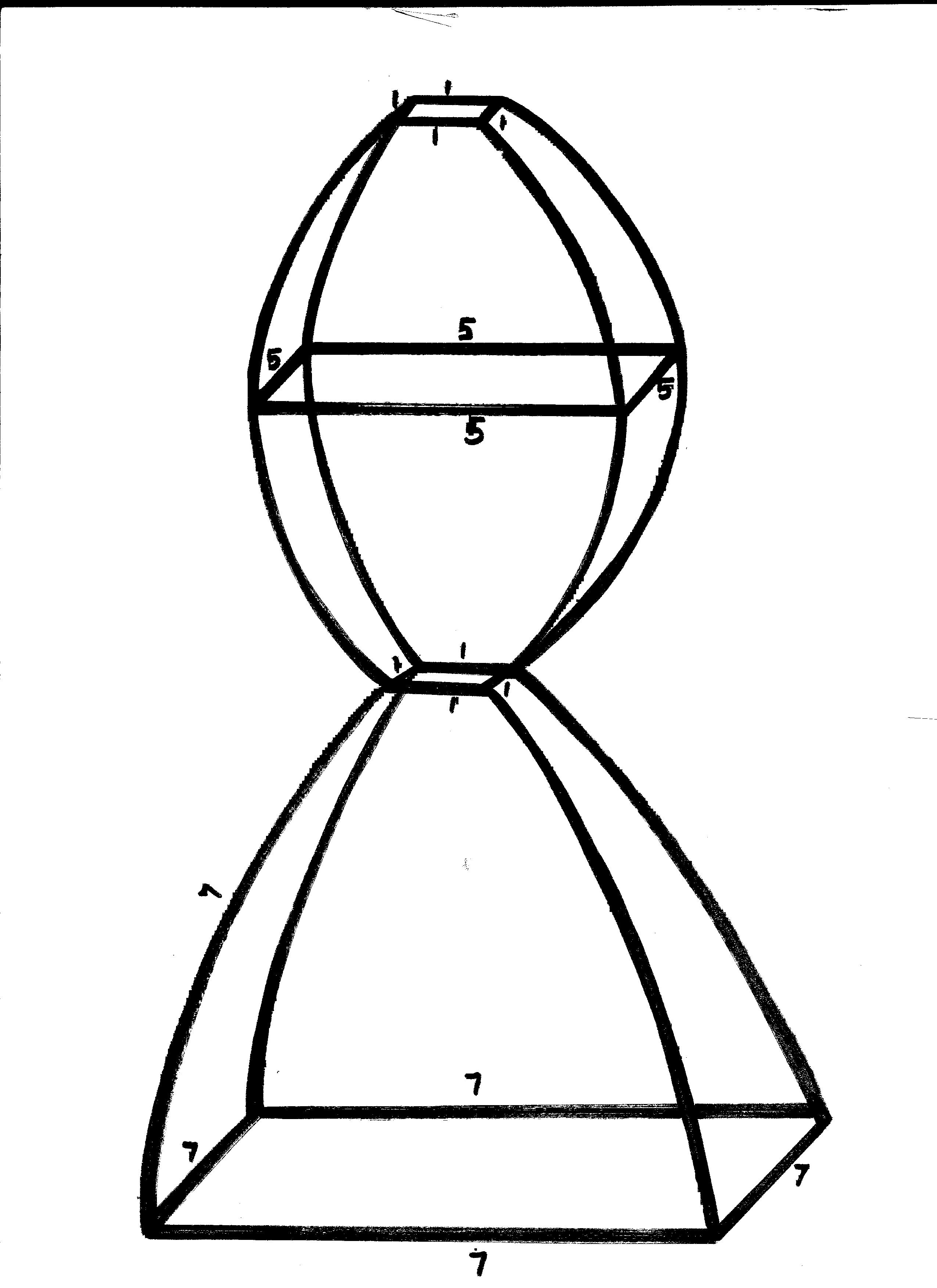
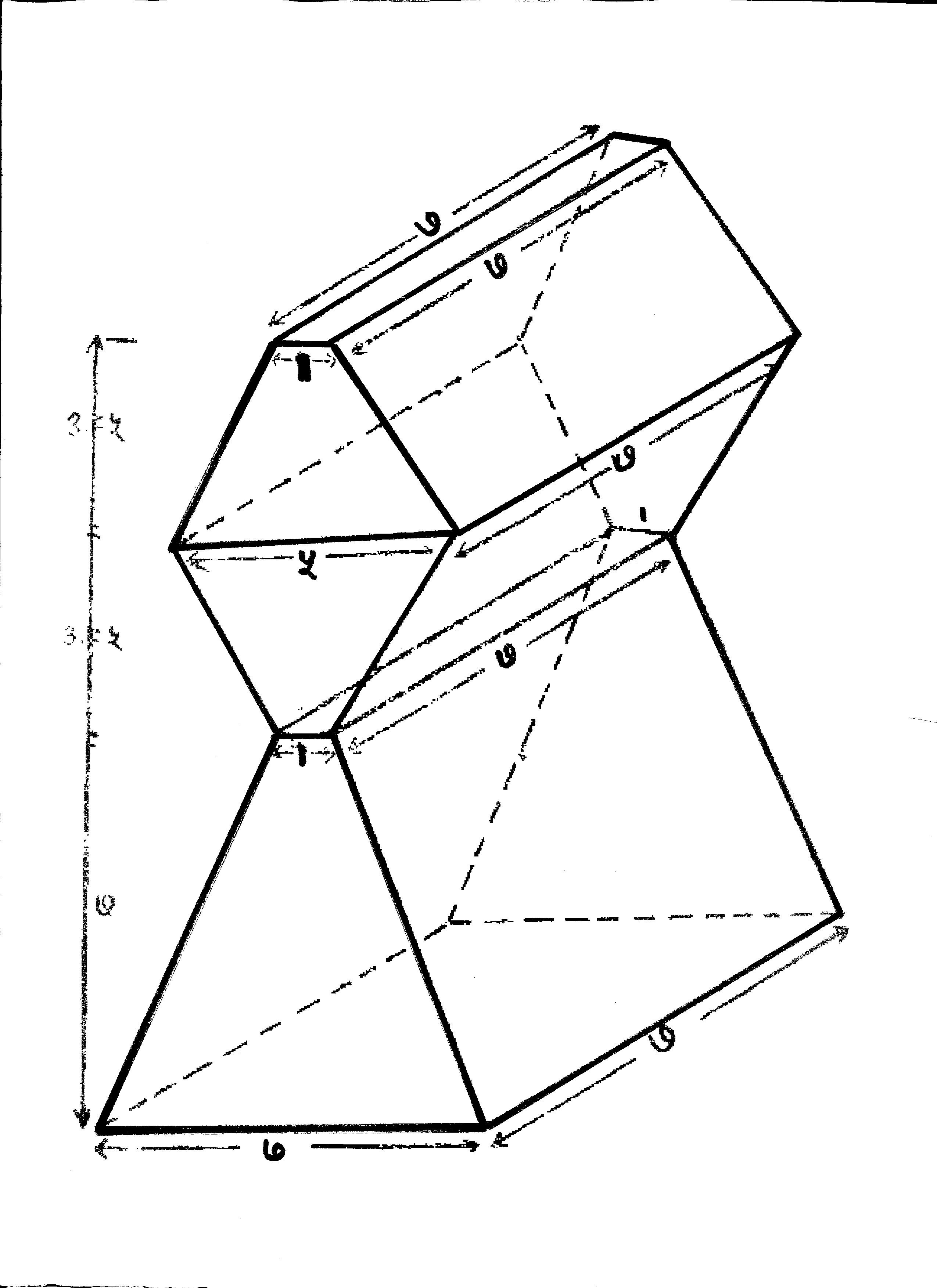
According to this philosophy, the Loka, Universe consists of six eternal substances i.e. Dravyas^[16] which produce the infinite world processes through their interactions. Each substance persists through its own modes.

Now, please permit me to be precise about each substance. For the subject is huge enough to be compressed in a few words. I therefore, strike at the core of the matter, without expatiating on it.

• Firstly, Dharmāstikāya - It is a kind of ether; it is the medium of all mobile constituents of the Universe. Remaining unmoved, It is a mover of the thing. It is additionally formless.
• Secondly, Adharmāstikāya - It is the medium of rest, the concomitant cause of all resting constituents of the Universe. It is formless.
• Thirdly, Ākāśāstikāya - That is space, the container of all other substances is itself self-contained. It is again, formless.
• Fourthly, Jīvāstikāya - Soul or physical order of existence, It, too is formless. Fifthly, Kāla - Needless to say, is the other name of Time.
• Sixthly, Pudgalāstikāya i.e. non soul, is a matter with form.

Precious information about Loka is found in the Jaina Books named Kṣetrasamāsa and Karaṇagāthā. Jinabhadra gaṇi (AD 550) wrote two works of the same class, a bigger one called Bṛhatkṣetrasamāsa and a smaller one called Laghukṣetrasamāsa. They furnish information as to the knowledge of geometry.

Small wonder, the cosmography of the Jainas, based on the various dimensions with geometrical precision, is for us Jainas, an illuminating experience. This is another alternative picture of the Loka, given by the Śwetāmbara sect. It is measured in Khaṇḍukas, not in Rajjus the previous one which I have shown you. The relationship between Khaṇḍukas, and Rajjus is that there are 4 Khaṇḍukas, in one Rajju.^[17] If we cut this Loka horizontally we can get various parallelepipeds of different sizes. Prof. Muni Mahendra Kumar throws light upon the mathematical explanation of the Loka (Universe), in his book named Viśva Prahelikā.

According to him if we regard this shape of the Loka, then we get its volume as 343 cubic Rajju, one Rajju is equal to innumerable Yojans.

The volume of the Loka has been derived on the basis of Euclidean Geometry. However, according to some Jain Treatises the geometry of the Loka is non-Euclidean. For example, while calculating the perimeter of the circular islands of the Loka, the value of Pie has been assumed to be a square root of ten. There is still a controversy, whether this measurement is the approximate value of pie or it has been taken according to Euclidean Geometry. Apart from it, if the shape of the Loka is a curved one then why cant we think that its geometry is non Euclidean. And if the geometry of Lokakāśa is non-Euclidean then it is necessary to get its volume according to non-Euclidean Geometry. Still, this is a subject of research.^[18]

As I come to the end of the lecture, I am quite unsure if I have done justice to search a subject, as I was invited to deliver a lecture on. I thank Prof. D.K. Sinha the president of AIMT. I also thank the respected audience present here. With this I sign off. Thank you.