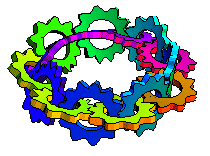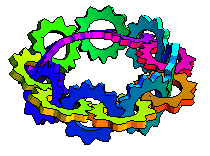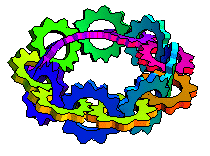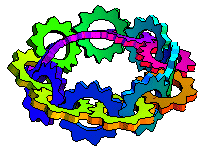Alex Bogomolny has started and still maintains a popular website "Interactive Mathematics Miscellany and Puzzles" to which he brought more than 10 years of college instruction and, at least as much, programming experience. He holds M.S. degree in Mathematics from the Moscow State University and Ph.D. in Applied Mathematics from the Hebrew University of Jerusalem.
His website
- Cut The Knot!
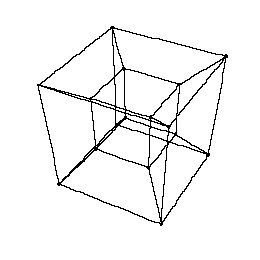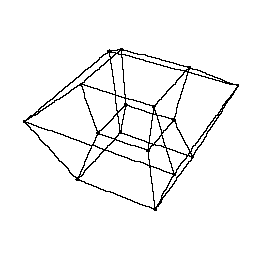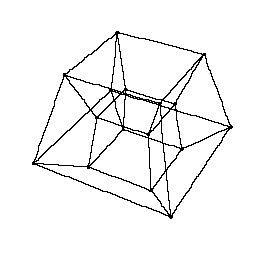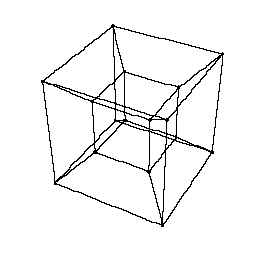
offers a java applet, which follows the dimensional construction line [0-1-2-3-4] we went through in the last chapters
and ends up with the graphic modell of a tesseract.
Following the instructions the applet offers a set set of parameters (sliders) which allows movements along all axes through hyperspace.
Try the options: "Fix origin", "Cross section", "Hyperplane"
Move the sliders slowly and watch the results meditatively.
If you read through the page you will find he is sharing a lot of humor on 4D travelling.
- Little down the page there is a second java applet to try out.
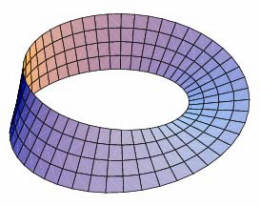
Here Mr. Alex Bogomolny mentions something very interesting about hyperplanes:Looking at the hyperplanes (squares of the cubes) inside the tesseract, he found out that those squares, having connections through a complete turn of a tesseract, are building a sequence along a moebius strip.
| ...To theWheels of Karma The mechanical interlocked turning gears symbolize perpetual cause & effect in an entangled closed loop.When we start to examine the process of "what moves what & which way" we have to go around the circle 2 times to reach the turning gear we started from. (passing 16 wheeling points). The basis for this special loop is the above mentioned moebius strip, which was invented independently around 1865 by 2 mathematicians, Moebius and Listing. The Möbius strip, also called the twisted cylinder, is a one-sided nonorientable surface obtained by cutting a closed band into a single strip, giving one of the two ends thus produced a half twist, and then reattaching the two ends. All we need is a piece of paper, scissors and a little bit of glue, to cut a strip, twist one end and glue it to the other end of the strip...
|
 Editor Aparigraha Jain
Editor Aparigraha Jain
 Editor Carla Geerdes
Editor Carla Geerdes