We get two equations in the Digambara tradition which indicate relations between time-units and space-units. In these equations, log2 is used. Modern name of Chedagaṇita is logarithms.[1]
In the first equation, the relationship between sūcī aṅgula (a linear space-unit) and addhā palyopama is described as follows:[2] sūcī aṅgula is equal to addhā palyopama raised to the power logarithm to the base2 addhā palyopama.
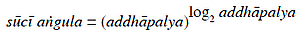
What should be the units of sūcī aṅgula and addhāpalya is not given here, but by logic (reasoning)[3] we find that they should be pradeśa and samaya because both of them are the units of measurement of space and time respectively. In this way, if sūcīaṅgula be x pradeśa and addhāpalya be 'p' samaya, then
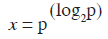
Second equation relates jagaśreṇī (the cosmic row of spaceunits which measures seven rajjus) and addhāpalya.[4] Jagaśreṇī is equal to ghanaṅgula (a three dimensional space-unit) raised to the power logarithm to the base two innumerableth fraction of addhāpalya.
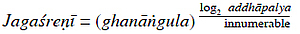
Here, ghanaṅgula means cube of sūcī aṅgula, i.e., cube of the number of pradeśas of sūcī aṅgula.
If Jagaśreṇī = 'j' pradeśa
and innumerable = a, then

Joining both the equations, we get:
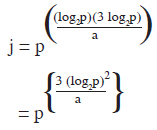
Explanation of Logarithms:
If logyk = a
then ay = k
y is called base.
Logarithm is written as log.
Log2 is the number which is attained by making half the number as many times as the number log2x is obtained, where x is the number log2.
 Prof. Muni Mahendra Kumar
Prof. Muni Mahendra Kumar

