Just as we know properties of photon or electron by using mathematical formulae, so also by the mathematical calculations, it is possible to compute the size of universe. The volume of the Universe can be found out if the radius of curvature of the Universe as a whole is known. Here it is necessary to distinguish between the curvature due to the local gravitational fields and the curvature of the universe as a whole. Whittaker has explained this thus: “The curvature to which Einstein’s original theory referred was a curvature variable from place to place. Now if we think of the earth’s surface, we recognize that owing to the existence of mountains and valleys, the amount of bending does in fact vary greatly from one locality to another. But over and above this, there is the bending which is what we usually mean when we talk of the curvature of the earth’s surface: that is the bending of the surface as a whole, when the mountains and valleys have been smoothed out, the bending which we refer to when we say that the earth is a globe of some 4000 miles radius. Similarly, in the case of the universe, we can suppose that all the small irregularities of curvature due to local gravitational fields have been smoothed out, and we can then ask, what is the curvature of the universe as a whole?”[1]
Now, the field-equations of Einstein give a relation between the radius of curvature and the mass of the bodies constituting the universe. It was assumed by Einstein that the universe is in exact equilibrium and the presence of matter produces a non-Euclidean metric that is a curvature of space.
Now if
R0 is the radius of curvature of the space which measures the departure from Euclidean metric;
M is the total mass of the particles constituting the universe;
γ Denotes the Newtonian constant of gravitation and
C is the velocity of light, then the equation
gives the relation between Ro and M.[2]
This equilibrium universe, which is called Einstein’s world, was discovered in 1917. Its total volume (which is finite) is given
Now, the average density of matter in the universe is given by
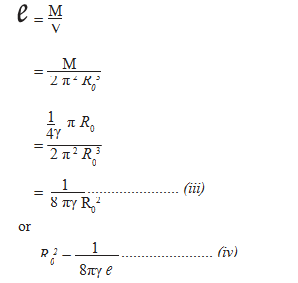
Thus, if the value of e is known, the value of R0 and hence the values of M and V also can be calculated.
Next, if we assume that the Einstein world is a reasonably good approximation to the actual universe, and if we make the further assumption that the average density of matter in the neighbourhood of our own cluster of galaxies (which would be e) then we have the equations from which the values of R0, M and V can be found. Thus we obtain estimates - very provisional and conjectural; it is true for the total mass of the universe and its total volume.[3]
 Prof. Muni Mahendra Kumar
Prof. Muni Mahendra Kumar



